Что значит иррациональные и трансцендентные числа

Какие числа называются иррациональными. Определение

Всякое рациональное число можно представить в виде m/n , где m и n - целые числа (положительные или отрицательные). Иррациональные числа в этом виде точно представить нельзя. Отсюда следует, что

Иррациональными числами называются такие числа, которые нельзя представить в виде m/n, где m и n - целые числа (положительные или отрицательные).

Но приближенно всякое иррациональное число можно с любой степенью точности заменить рациональным числом m/n; в частности, можно найти десятичную дробь (правильную или неправильную), как угодно мало отличающуюся от данного иррационального числа.

Числа √2, √5, ³√3 + √2, √³√5 + √7

и многие другие выражения, содержащие рациональные числа под знаком радикала, иррациональны. Эти иррациональные числа называются «выражающимися через радикалы».

Однако ими далеко не исчерпывается запас иррациональных чисел. До конца 18 века математики были убеждены, что корень всякого алгебраического уравнения с рациональными коэффициентами, если этот корень не рационален, можно выразить через радикалы; затем было доказано, что это верно лишь для уравнений до 4-й степени включительно. Иррациональные корни уравнений, 5-й и высших степеней, как правило, не могут быть выражены через радикалы. Числа, являющиеся корнями алгебраических уравнений с целыми коэффициентами, называются алгебраическими числами; лишь в исключительных случаях алгебраические числа выражаются радикалами; еще реже они рациональны.

Возникновение иррациональных чисел

Одной из причин приведшей к возникновению иррациональных чисел стала нехватка для теории измерений существующего набора целых и дробных чисел достаточных для измерительной практики. Поясним это на следующем примере.

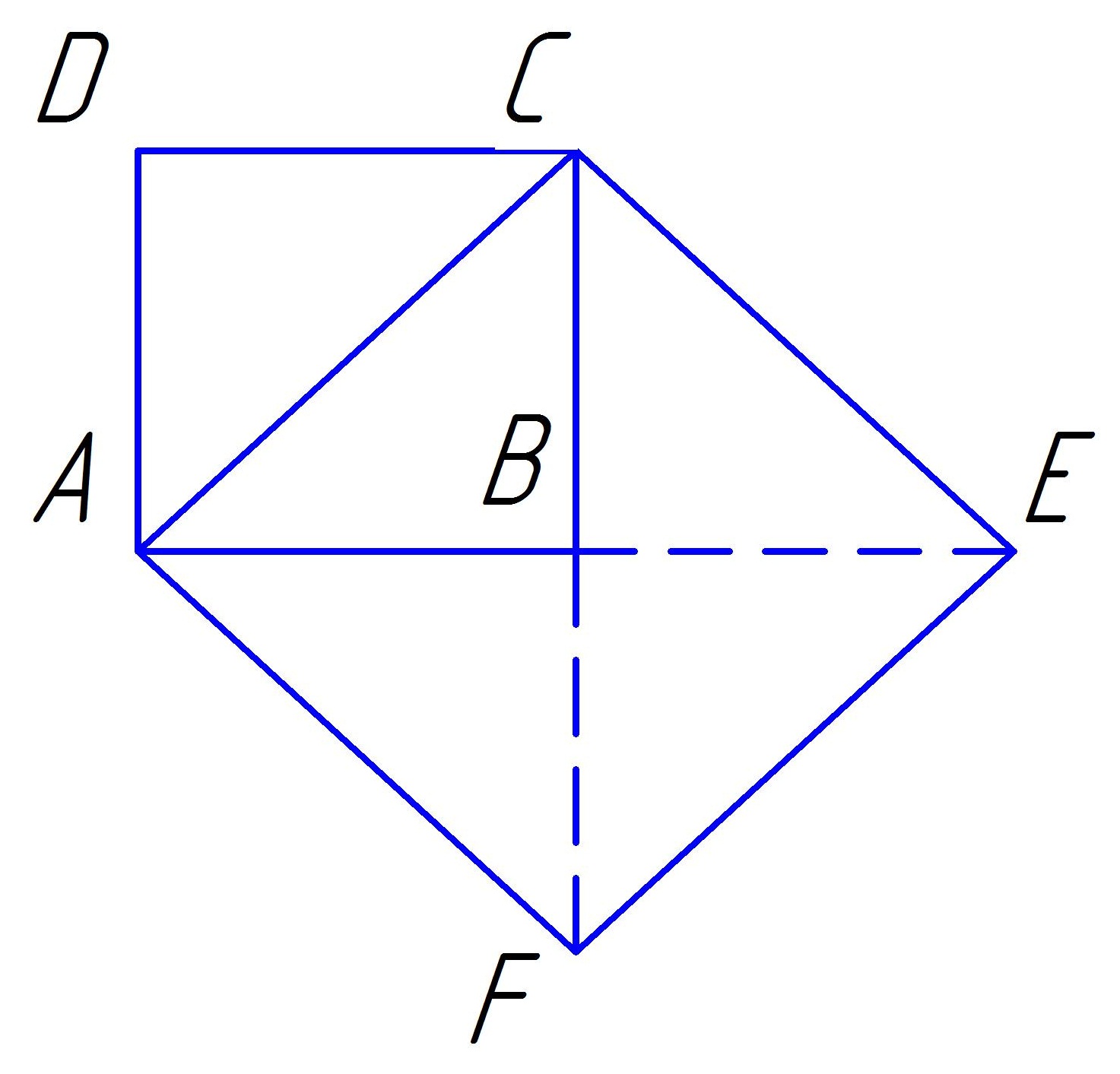
Пусть, например, требуется точно определить длину диагонали АС квадрата ABCD (фиг. 1), сторона которого равна 1 м. Площадь квадрата ACEF, построенного на диагонали, равна удвоенной площади АВСD (треугольник АСВ содержится в АВСD два раза, а в ACEF - четыре). Поэтому, если х есть искомая длина АС, то должно быть х² = 2. Но никакое целое и никакая дробь не могут удовлетворить этому уравнению.

Остается одно из двух: или отказаться от точного выражения длин числами, или ввести новые числа, сверх целых и дробных. После длительной борьбы этих двух точек зрения победила вторая.

Числа нового рода, представляющие длины отрезков, несоизмеримых с единицей масштаба (т. е. отрезков, которые нельзя выразить целым или дробным числом), называются иррациональными*. В противоположность иррациональным числа целые и дробные получили название рациональных. После введения отрицательных чисел (оно произошло позднее) и среди них стали различать рациональные и иррациональные.

Трансцендентные числа

Но и алгебраические числа не исчерпывают запаса иррациональных чисел. Так, например, известное из геометрии число π иррационально, но не может быть корнем никакого алгебраического уравнения с целыми коэффициентами. Точно так же число е не является алгебраическим. Иными словами π и е не алгебраические числа.

Иррациональное число, не могущее быть корнем никакого алгебраического уравнения с целыми коэффициентами, называется трансцендентным числом.

До 1929 г. лишь для немногих чисел была доказана их трансцендентность; трансцендентность числа е была доказана в 1871 г. французским математиком Эрмитом. В 1882 г. немецкий математик Линдеман доказал трансцендентность числа π. Академик А. А. Марков (1856-1922) доказал трансцендентность чисел е и π новым методом. В 1913 г. Д. Д. Мордухай - Болтовской (1877-1952) указал ряд новых трансцендентных чисел. Однако все еще оставалось неизвестным, трансцендентны ли такие «обыкновенные» числа, как 3^√2, √3^√2

Советский математик А. О. Гельфонд (род. 1906 г.) в 1934 г. доказал трансцендентность всех чисел вида α^β — любые алгебраические числа (при условии, что α не равно 0 или 1, а β иррационально). Например, (⁴√5)^3√2

число трансцендентно. Из трансцендентности чисел α^β легко вытекает трансцендентность десятичных логарифмов всех целых чисел (конечно, кроме 1, 10, 100, 1000 и т. д.).

*Термин «иррациональный» дословно означает «не имеющий отношения». Первоначально его относили не к иррациональному числу, а к тем величинам, отношение которых мы сейчас выражаем иррациональным числом. Например, отношение диагонали квадрата к его стороне мы сейчас представляем числом √2. До того, как были введены иррациональные числа, говорили, что диагонали квадрата не имеют отношения к его стороне.