Логарифм

Логарифмом числа N по основанию а (обозначается log_aN) называется показатель степени, в которую надо возвести число а, чтобы получить число N, т. е. b = log_aN, если а^b = N.

Логарифм определен для любого положительного числа N при любом отличном от единицы положительном основании а. Каждому положительному числу при данном основании соответствует единственный логарифм.

По определению логарифма справедливо равенство

а^log_aN = N,

из которого на основе свойств показательной функции устанавливаются основные свойства логарифмов (здесь М, N и к-положительные числа):

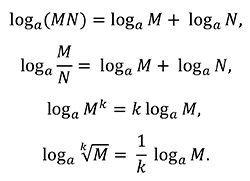
Эти свойства позволяют сводить умножение и деление чисел (представленных в виде степеней некоторого числа, принятого за основание) к сложению и вычитанию показателей степеней, а возведение в степень и извлечение корня-к умножению и делению на показатель степени, поэтому применение логарифмов упрощает и сокращает сложные вычисления.

При нашей десятичной системе счисления самым удобным основанием является число 10. Логарифм по основанию 10 называется десятичным логарифмом и обозначается lg:

lg N = log₁₀N

При основании, равном 10, только логарифмы целых степеней числа 10 представляются целыми числами (lg 10³ = 3, lg 0,01 = lg l0^-2 = - 2), логарифмы же остальных чисел представляются дробями, и в таблицах даются их приближенные значения в виде конечных десятичных дробей, например lg 25,43 = 1,4053. Целая часть значения логарифма называется характеристикой, дробная - мантиссой.

Любое положительное число N всегда можно представить в виде N = 10ⁿ * х, где n-целое число, а х заключено в пределах от 1 до 10. Заметим, что lg 1 = 0, lg 10 = 1, а для любого числа х, заключенного между 1 и 10 его логарифм заключен между нулем и единицей: 0 ≤ lgx < l. Из этого представления числа N следует, что lg N = п + lg х,

где n - характеристика, a lg X-мантисса логарифма числа N.

Характеристику числа определяют по его виду. Для числа, большего единицы, характеристика на единицу меньше числа цифр у целой части этого числа. Для числа, заключенного между нулем и единицей и записанного десятичной дробью, характеристика отрицательна и равна взятому со знаком минус числу нулей до первой значащей цифры, например для числа 0,0216 его характеристика равна — 2. Благодаря такому простому способу определения характеристики в таблицах даются одни мантиссы.

Логарифмы были введены шотландским математиком Дж. Непером (1550-1617) и независимо от него швейцарским механиком и математиком И. Бюрги (1552-1632). Бюрги пришел к логарифмам раньше, но опубликовал свои таблицы с опозданием (в 1620 г.), и первой в 1614 г. появилась работа Непера "Описание удивительной таблицы логарифмов". Основанием таблицы логарифмов Непера является иррациональное число, к которому неограниченно приближаются числа вида (1 + 1/n)ⁿ при безграничном возрастании n. Это число называют неперовым числом и со времен Л.Эйлера обозначают буквой е:

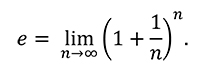
Непер составил таблицы, взяв очень хорошее приближение числа е, а именно (1 + 1/10⁷)¹⁰⁷. Логарифмы по основанию е называются натуральными логарифмами и обозначаются ln (образовано от первых букв слов "логарифм натуральный").

Первые таблицы десятичных логарифмов были составлены необыкновенно изобретательным и остроумным вычислителем, английским математиком Г. Бриггсом (1561-1630). Его "логарифмическая арифметика" содержала четырнадцатизначные таблицы для чисел от 1 до 20 000 и от 90 000 до 100 000. Голландский математик А. Флакк (1600-1667) заполнил пробелы бриггсовых таблиц, напечатав в 1628 г. таблицы логарифмов всех чисел от 1 до 100 000 с десятью знаками в мантиссе. Эти таблицы стали выпускаться во многих странах мира. На русском языке первые логарифмические таблицы были изданы в 1703 г.