Возведение в степень и извлечение квадратного корня из приближенных чисел

Возведение в (целую) степень есть повторное умножение и потому к нему относится все сказанное ранее. При возведении в небольшую степень результат имеет столько же точных цифр, сколько взятое число, или содержит небольшую ошибку в последнем знаке. Если степень велика, накопление небольших ошибок может отразиться и на цифрах высшего разряда.
При извлечении корня результат имеет столько же верных цифр, сколько их было в подкоренном числе*.
Излагаемый в школьных учебниках способ извлечения корня громоздок и трудно запоминается. Вот простой и легко, запоминаемый способ**, который предпочтительно применять при вычислении на три-четыре знака (большее число знаков редко нужно для практики).
Правило извлечения корня. Берем «на-глаз» приближенную величину корня.
1) Делим на нее подкоренное количество.
2) Полусумма полученного частного и первоначально взятого приближения дает значительно более-точный результат. Если этой точности недостаточно, повторяем тот же процесс, беря вместо первого приближения полученное нами более точное.
Пример 1.. В подкоренном числе три точные, цифры; в корне нет смысла вычислять более трех цифр. За первое приближение возьмем ≈ 5,00
(23,5 значительно ближе к 25 = 5², чем к 16 = 4²).
Делим подкоренное число 23,5 на первое приближение 5, доводя деление до третьего знака: 23,5: 5 = 4,70. 1) Берем полусумму найденного числа 4,70 и первоначально взятого приближения 5,00;

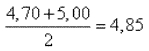
Так как числа 4,70 и 5,00 не сильно отличаются друг от друга, то в полученном результате ≈ 4,85
все цифры должны быть верны. Полную гарантию в этом получим при повторении процесса. Вместо первого приближения 5 возьмем более точное значение
≈ 4,85. Делим 23,5:4,85 ≈ 4,85. Равенство делимого и частного с точностью до третьего знака гарантирует правильность трех знаков результата.
Пример 2. За первое приближение берем 1,5 (2,35 примерно одинаково отстоит от 1 = 1² и от 4 = 2²).
1) 2,35:1,50 ≈ 1,57. 2). 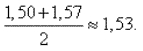Все три знака верны, так как числа 1,50 и 1,57 очень мало отличны друг от друга. Если известно, что подкоренное число есть 2,350, то чрезвычайная близость чисел 1,50 и 1,57 позволит, сразу же найти и четвертый знак результата:
1) 2,350:1,500 = 1,567.
2)
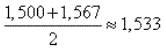
Имеем:
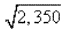≈ 1,533
Все четыре знака верны.
Когда подкоренное число — десятичная дробь, имеющая небольшую целую часть или вовсе ее не содержащая, то при подыскании первого приближения рекомендуется переносить запятую через четное число цифр вправо. После того все действия можно выполнять, не обращая внимания на место запятой. Место запятой в результате определяется по грубому подсчету. Если пользоваться сокращенными приемами деления и вычисления полусуммы, результат находится очень быстро.
Пример 3.
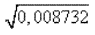
Перенося запятую через четыре знака вправо, имеем 87,32. Учитывая две первые цифры 87, находим грубое приближение 9.
1) Не обращая, внимания на запятые, делим 8732:9 ≈ 970,2. Отбросив запятую в этом результате, имеем четырехзначное число 9702.
2) Взяв первое приближение (9) с тем же числом знаков (9000), находим полусумму

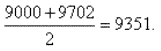
Расхождение между 9000 и 9702 велико; поэтому лишь три знака в числе 9351 верны. Чтобы получить четвертый знак,повторяем этот процесс:
1) 8732:9351 ≈ 0,9338;
2)
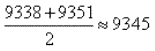
Все четыре знака верны. Запятую ставим по округлению (соображая, что
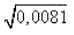≈ 0,09). Окончательно имеем:
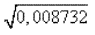≈ 0,09345.
Пример 4.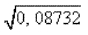Перенося запятую через два знака вправо, имеем 8,732 (или через четыре; тогда имеем 873,2, но не 87,32, как в предыдущем примере).Первое приближение
≈ 3.
1) Делим 8732:3 ≈ 2911.
2) 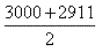≈ 2955.
Все четыре знака верны. Ставя запятую по грубому округлению ( 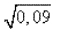= 0,3), имеем
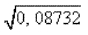≈ 0,2955.



*Если при извлечении квадратного корня подкоренное число имеет, например, три значащие цифры, то, извлекая из него корень, мы можем получить не менее трех верных знаков. Пользуясь способом, излагаемым обычно в учебниках (разбивка на грани), мы для этого будем должны к подкоренному числу дописать два или три нуля. Эти нули будут неточными цифрами, но соответствующие цифры результата будут точны. Те же цифры мы получим, если вместо нулей допишем любые цифры.

**Излагаемый ниже способ описан дневнегреческим математиком Героном примерно 2000 лет назад. Герон пользовался простыми дробями.