Логарифмический метод, смысл логарифма, таблица логарифмов
Умножение, деление, возведение в степень и извлечение корня - действия, гораздо более трудоемкие, чем сложение и вычитание, особенно тогда, когда нужно производить действия с многозначными числами. Настоятельная потребность в таких действиях впервые возникла в 16 веке в связи с развитием дальнего мореплавания, вызвавшим усовершенствование астрономических наблюдений и вычислений. На почве астрономических расчетов и возникли на рубеже 16 и 17 веков логарифмические вычисления.
В настоящее время эти вычисления применяются повсюду, где приходится иметь дело с многозначными числами. Они выгодны уже при действиях с четырехзначными числами и совершенно необходимы в тех случаях, когда точность должна доходить до пятого знака. Большая точность на практике требуется очень редко.
Ценность логарифмического метода состоит в том, что он сводит умножение и деление чисел к сложению и вычитанию - действиям менее трудоемким. Возведение в степень, извлечение корня, а также ряд других вычислений (например, тригонометрических) также значительно упрощаются. Выясним на примерах идею логарифмического метода.
Пусть требуется помножить 10 000 на 100000. Конечно, мы не станем выполнять этого действия по схеме умножения многозначных чисел. Мы просто сосчитаем число нулей в множимом (4) и множителе (5), сложим эти числа (4 + 5 = 9) и сразу напишем произведение 1000000000 (9 нулей). Законность такого вычисления основана на том, что сомножители суть (целые) степени числа 10: множится 104 на 105; при этом показатели степеней складываются. Точно так же сокращенно выполняется и деление степеней десяти (деление заменяется вычитанием показателей). Но так можно делить и умножать лишь немногие числа; например, в пределах первого миллиона можно брать (не считая 1) лишь 6 чисел: 10, 100, 1000, 10 000, 100 000, 1 000 000. Чисел, допускающих подобное умножение и деление, будет гораздо больше, если взять вместо основания 10 другое, более близкое к 1. Возьмем, например, основание 2 и составим таблицу его первых 12 степеней, показатель степени.
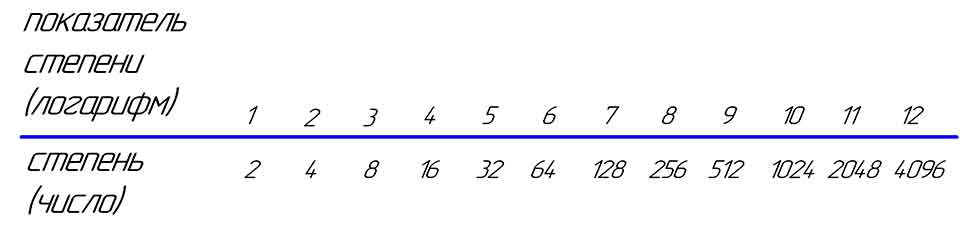
Числа, стоящие в верхней строке (показатели степеней), мы будем теперь называть логарифмами, а числа, стоящие в нижней строке (степени), - просто числами.
Чтобы перемножить какие-либо два числа нижней строки, достаточно сложить два числа, стоящих над ними. Например, чтобы найти произведение 32 и 64, сложим стоящие над 32 и над 64 числа 5 и 6; 5 + 6=11. Под числом 11 находим результат: 2048. Чтобы разделить 4096 на 256, возьмем числа 12 и 8, стоящие над ними; вычитаем: 12 – 8 = 4. Под числом 4 находим ответ: 16. Если продолжить таблицу влево, введя нулевую и отрицательную степени числа 2, то можно будет выполнять и деление меньших чисел на большие.
Хотя среди степеней числа 2 гораздо меньше пробелов, чем среди степеней числа 10, все же в нижней строке нашей таблицы нет очень многих чисел. Поэтому практического значения и эта таблица не может иметь. Но если за основание взять число, гораздо более близкое к 1, чем число 2,. то этот дефект будет устранен.
Примем, например, за основание число 1,00001. В пределах между 1 и 100 000 окажется свыше миллиона (1 151 292) его последовательных степеней. Если мы округлим значения этих степеней, сохранив лишь шесть значащих цифр, то среди миллиона округленных результатов окажутся все целые числа от 1 до 100 000. Правда, это будут лишь приближенные значения степеней. Но так как при умножении и делении пятизначных целых чисел нас будут интересовать только первые пять знаков результата, то составленные таблицы позволят перемножать, делить и т. д. пятизначные целые числа, а следовательно, и десятичные дроби, имеющие пять значащих цифр.
Именно так и были составлены первые таблицы логарифмов*. Вычисление их потребовало многолетней неутомимой работы. В настоящее время методами высшей математики эту работу мог бы выполнить каждый в течение какого-нибудь месяца. Триста лет назад этому нужно было посвятить всю жизнь. Но зато во много раз возросла производительность труда многих тысяч вычислителей, пользовавшихся раз навсегда составленными таблицами.
В настоящее время в таблицах логарифмов кладется в основание число 10, что дает ряд вычислительных преимуществ (так как наша нумерация — десятичная). При этом для получения целых чисел приходится брать дробные степени числа 10. Логарифм некоторого числа при основании 10 называется его десятичным логарифмом. Составление таблицы десятичных логарифмов не представляет особых трудностей, если уже составлена таблица по основанию 1,00001. Действительно, пусть мы хотим найти десятичный логарифм числа 3, т. е. тот показатель степени, в которую нужно возвести 10, чтобы получить 3. Из таблицы по основанию 1,00001 мы найдем:
10 ≈ 1,00001230258, 3 ≈ 1,00001109861
Возведя обе части первого равенства в степень 1/230258 найдем: 1,00001 ≈ 101:2302588; поэтому второе равенство перепишется в виде 3 ≈ 10(109861:230585), т. е. десятичный логарифм числа 3 есть 0,47712. Подобным же образом можно найти десятичные логарифмы и остальных чисел**.
*Швейцарцем Бюрги (ок. 1590 г.); несколько позднее независимо от Бюрги были составлены таблицы логарифмов шотландцем Непером, который брал за основание число, очень близкое к единице, но меньшее чем единица. Бюрги опубликовал свою работу лишь в 1620 г., раньше (в 1611 г.) - появились в свет таблицы Непера.
**Идея составления таблицы десятичных логарифмов принадлежит Неперу и его сотруднику англичанину Бриггу. Они совместно начали работу по пересчету прежних таблиц Непера на новое основание 10. После смерти Непера Бригг продолжил и закончил эту работу (он опубликовал ее полностью в 1624 г.). Поэтому десятичные логарифмы называются иначе бригговими. Дробные степени в то время еще не были приняты в математике, но Непер и Бригг обходились без них, так как понятию логарифма они давали определение, несколько отличающееся от ныне принятого
