Геометрический смысл умножения комплексных чисел
Пусть два комплексных числа z и z' изображаются векторами ОМ и OM' (фиг. 12). Запишем сомножители в тригонометрической форме и вычислим произведение:
zz' = r (cosφ + isinφ) • r'(cosφ' + isinφ') =
= rr' [(cosφ cosφ' - sinφ sinφ') + (sinφ cosφ ' + cosφ sinφ')],
т. e.
zz' = rr' [cos (φ + φ) +i'sin (φ'+ φ')]. (1)
Модуль произведения (оно изображено вектором OL), есть rr', а аргумент произведения равен φ + φ'» т. е. при умножении комплексных чисел их модули
перемножаются, а аргументы складываются.
Это правило остается в силе для любого числа сомножителей.
![]() Пример 1. У комплексных чисел, изображенных векторами ОМ и ОМ' фиг. 12, модули
равны |ОМ| = и |ОМ'| = 2, а аргументы
Пример 1. У комплексных чисел, изображенных векторами ОМ и ОМ' фиг. 12, модули
равны |ОМ| = и |ОМ'| = 2, а аргументы ![]() ХОМ = 20° и ХОМ' = 30°. Модуль произведения,
Модуль произведения, изображенного вектором OL есть 3/2 • 2 = 3; аргумент произведения (угол XOL) равен
ХОМ = 20° и ХОМ' = 30°. Модуль произведения,
Модуль произведения, изображенного вектором OL есть 3/2 • 2 = 3; аргумент произведения (угол XOL) равен
(cos 20° +i sin 20°) • (cos 30° + isin 30°) = 3 (cos 50° + i sin50°).
4
Те же сомножители в алгебраической форме будут 4 + 4i и -1i/2 + 1i/2 . Перемножив, снова найдем - 4.
Пример 3. Перемножить 2(cos 150° + isin 150°),
3 [cos ( - 160°) + isin ( - 160°)] и 0,5 (cos 10° + isin 10°).
Модуль произведения 2 • 3 • 0,5 = 3. Аргумент произведения 150° - 160° + 10° = 0°. Произведение равно
3 (cos 0° + isin 0°) = 3.
Пример 4. r (cosφ + i sinφ) • r [cos(-φ) + isin(-φ) = r2 (cos 0° + isin 0°) = r2, т. е. произведение двух сопряженных комплексных чисел есть действительное число, равное квадрату их общего модуля.
Пример 5.
3/2[cos(-20°)+isin(-20°)]•2[cos(-30°)+isin(-30°)] = 3[cos(-50°) +isin(-50°)].
 Замечание 1. Правила умножения действительных чисел оказываются частным случаем вышеприведенного правила. Так, при перемножении двух чисел - 2 и - 3
аргументы их (180° и 180°) дают в сумме 360°, так что произведение есть положительное число 6 [т. е. 6 (cos 360° + i sin 360°)].
Замечание 2. Когда какое-либо комплексное число r (cosφ + isinφ) умножается на мнимую единицу i (модуль ее есть 1, а аргумент + 90°), то
модуль произведения остается равным r. Аргумент же увеличивается на 90°, т. е. вектор множителя поворачивается на угол + 90°, не меняясь по длине.
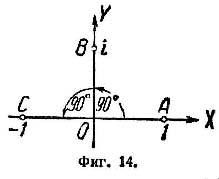
В частности, умножение 1 (вектор ОА фиг. 14) на i представляется поворотом вектора ОА на 90° в положение OS, а умножение i на i представляется
поворотом ОВ на 90° в положение ОС. Но вектор ОС изображает -1. Поэтому i2 = -1. В этой геометрической картине число i
является «мнимым» не в большей степени, чем число -1.
Замечание 1. Правила умножения действительных чисел оказываются частным случаем вышеприведенного правила. Так, при перемножении двух чисел - 2 и - 3
аргументы их (180° и 180°) дают в сумме 360°, так что произведение есть положительное число 6 [т. е. 6 (cos 360° + i sin 360°)].
Замечание 2. Когда какое-либо комплексное число r (cosφ + isinφ) умножается на мнимую единицу i (модуль ее есть 1, а аргумент + 90°), то
модуль произведения остается равным r. Аргумент же увеличивается на 90°, т. е. вектор множителя поворачивается на угол + 90°, не меняясь по длине.
В частности, умножение 1 (вектор ОА фиг. 14) на i представляется поворотом вектора ОА на 90° в положение OS, а умножение i на i представляется
поворотом ОВ на 90° в положение ОС. Но вектор ОС изображает -1. Поэтому i2 = -1. В этой геометрической картине число i
является «мнимым» не в большей степени, чем число -1.