Геометрический смысл сложения и вычитания комплексных чисел

Пусть векторы ОМ и ОМ' (фиг. 7) изображают комплексные числа z = x + yi и z'=x' + y'i. Из точки M проведем вектор МК, равный ОМ' (т. е. имеет ту же длину и то же направление, что ОМ'). Тогда вектор ОК изображает сумму данных комплексных чисел*.
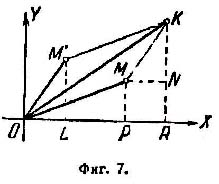Построенный указанным образом вектор ОК называется геометрической суммой (или, короче, суммой) векторов OM и ОМ' (название «сумма» проистекает из того, что совершенно таким же образом складываются скорости движущихся тел, силы, приложенные к одной точке, и многие другие физические величины). Итак, сумма двух комплексных чисел представляется суммой векторов, изображающих отдельные слагаемые.
Длина стороны ОК треугольника ОМК меньше суммы и больше разности длин ОМ и МК. Поэтому

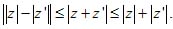
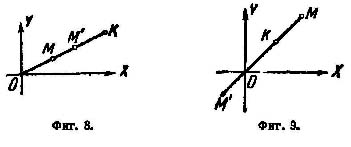
Равенство имеет место только в тех случаях, когда векторы OM и OM' имеют одинаковые (фиг. 8) или противоположные направления (фиг. 9).
В первом случае |OM|+|OM'|=|OK|, т.е. |z + z'| = |z| + |z'|.
Во втором |z| + |z'| = ||z| - |z'||.
Пример 1. Пусть z=4+3i; z'= 5+12i.
Тогда
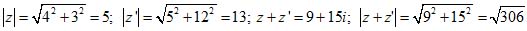
Имеем 13 – 5 < <13 + 5, т.е. 8 < < 18.
Пример 2. Пусть z = 4 + 3i; z' = 8 + 6i. Эти комплексные числа имеют один и тот же аргумент (36˚52'), т. е. соответствующие векторы имеют одинаковые направления. Здесь |z| = 5; |z'|=10; z + z'= 12 +9i;
Имеем 10 – 5 < 15 = 10 + 5.
Пример 3. Пусть z = 8 – 6i; z' = - 12 + 9i. Эти комплексные числа изображаются векторами, имеющими противоположные направления (их аргументы равны 323˚08' и 143˚08'). Здесь

|z| = 10; |z'| = 15; z + z' = -4 + 3i; |z + z'| = 5.
15 – 10 = 5 <15 + 10.
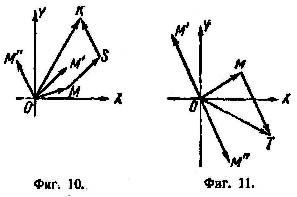
Сумма трех (и большего числа) комплексных чисел также представляется суммой векторов (ОМ, ОМ', ОМ" на фиг. 10), изображающих отдельные слагаемые, т. е. вектором ОК, замыкающим ломаную OMSK (вектор MS paвен вектору ОМ', вектор SK - вектору ОМ"). Слагаемые можно брать в любом порядке; ломаные будут различные, но концы их совпадут. Так как ОК не длиннее, чем ломаная OMSK, то

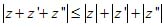
Равенство имеет место только тогда, когда все слагаемые имеют одно и то же направление.
Разность между комплексными числами a + bi и а' + b'i сумме чисел a + bi и - а' - b'i. Второе слагаемое имеет тот же модуль, что а'+b'i, но противоположное направление. Поэтому разность комплексных чисел, представляемых векторами ОМ и ОМ' (фиг. 11), изображается суммой векторов ОМ и ОМ" (вектором ОТ).