Геометрическое изображение комплексных чисел

Действительные числа можно изобразить точками прямой линии, как показано на фиг. 2, где точка А изображает число 4, а точка В – число – 5. Эти же числа можно изображать также отрезками ОА, ОВ, учитывая не только их длину, но и направление.

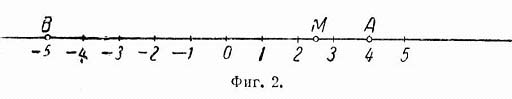
Каждая точка М «числовой прямой» изображает некоторое действительное число (рациональное, если отрезок ОM соизмерим с единицей длины, и иррациональное, если несоизмерим).

Таким образом, на числовой прямой не остается места для комплексных чисел.

Но комплексные числа можно изобразить на «числовой плоскости». Для этого мы выбираем на плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях (фиг. 3). Комплексное число a +bi мы изображаем точкой М, у которой абсцисса х (на фиг. 3 х = ОР = QM) равна абсциссе а комплексного числа ордината у (ОQ = РМ) равна ординате b комплексного числа.

Пример 1. На фиг. 4 точка A с абсциссой х = 3 и ординатой у = 5 изображает комплексное число 3 + 5i . Точка В изображает комплексное число – 2 + 6i; точка C комплексное число – 6 – 2i; точка D – комплексное число 2 – 6i.

Действительные числа (в комплексной форме они имеют вид a + 0i) изображают точками оси X, а чисто мнимый (вида 0 + bi) – точками оси Y.

Примеры 2. Точка К на фиг. 4 изображает действительное число 6 (или, что то же, комплексное число 6 + 0i), точка L — чисто мнимое число 3i (т. е. 0 + 3i); точка N - чисто мнимое число – 4i (т. е. 0 – 4i). Начало координат изображает число 0 (т. е. 0 + 0i ).

Сопряженные комплексные числа изображаются парой точек, симметричных относительно оси абсцисс; так, точки С и С' на фиг. 4 изображают сопряженные числа – 6 – 2i и – 6 + 2i. Комплексные числа можно изображать также Отрезками («векторами»), начинающимися в точке О и оканчивающимися в соответствующей точке числовой плоскости. Так, комплексное число – 2 + 6i можно изобразить не только точкой В (фиг. 4), но также вектором ОB; комплексное число - 6 – 2i изображается вектором ОС и т. д.

ПРИМЕЧАНИЕ. Давая какому-либо отрезку наименование «вектор», мы подчеркиваем, что существенное значение имеет не только длина, но и направление отрезка. Два вектора считаются одинаковыми (равными) только в том случае, когда они имеют одинаковую длину и одно и то же направление.