Деление комплексных чисел
В соответствии с определением деления действительных чисел устанавливается следующее определение.
Определение. Разделить комплексное число а +bi (делимое) на комплексное число а' + b'i (делитель) - значит найти такое число x+yi (частное), которое, будучи помножено на
делитель, даст делимое.
Если делитель не равен нулю, то деление всегда можно; и частное единственно (доказательство см. в замечании 2). На практике частное удобнее всего находить следующим образом.
Пример 1. Найти частное (7 – 4i) : (3 + 2i).
Записав дробь ![]() , расширяем её на число 3 – 2i, сопряженное с 3 +2i.Получим:
, расширяем её на число 3 – 2i, сопряженное с 3 +2i.Получим:
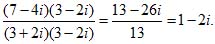
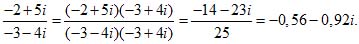 Пример 3.
Пример 3.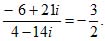 Здесь проще всего сократить на (-2 + 7i).
Поступая, как в примерах 1 и 2, найдем общую формулу:
Здесь проще всего сократить на (-2 + 7i).
Поступая, как в примерах 1 и 2, найдем общую формулу:
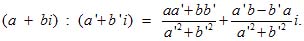 (1)
(1)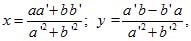
 ), т.е. если a'2 + b'2 ≠ 0.
Остается рассмотреть случай а'2 + 6'2 = 0. Он возможен лишь тогда (числа а' и b' действительны!), когда а' = 0 и b' = 0, т. е, когда делитель а' + b'i
равен нулю.
), т.е. если a'2 + b'2 ≠ 0.
Остается рассмотреть случай а'2 + 6'2 = 0. Он возможен лишь тогда (числа а' и b' действительны!), когда а' = 0 и b' = 0, т. е, когда делитель а' + b'i
равен нулю.
Если при этом и делимое а + bi равно нулю, то частное неопределенно. Если же делимое не равно нулю, то частное не существует (говорят, что оно равно бесконечности).
