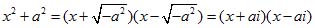Разложение квадратного трехчлена на множители
Квадратный трехчлен ах2 + bx + с можно разложить на множители первой степени следующим образом: решим квадратное уравнение ах2 + bх + с = 0.
Если x1 и x2 — корни этого
уравнения, то ах2+bx+с = а (х - х1) (х - х2).
Пример 1. Разложить на множители (первой степени трехчлен 2х2 + 13x -24. Решаем уравнение 2х2+ 13x -24= 0.
Находим корни: x1 = ; x2 = - 8.
Следовательно,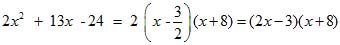
Пример 2. Разложить на множители х2 +a2; уравнение х2 +a2 = 0 имеет мнимые корни
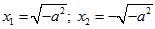, поэтому разложить х2 +a2 на действительные множители первой степени нельзя. На
мнимые множители он разлагается так:
).