Пропорции
Определение отношения и пропорции смотрите в разделе Арифметика , раздел 47. Из пропорции
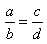 вытекает ad=bc (произведение средних членов равно произведению
крайних); обратно, из ad=bc вытекают пропорции
вытекает ad=bc (произведение средних членов равно произведению
крайних); обратно, из ad=bc вытекают пропорции
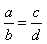 ;
;
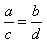 ;
;
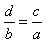
и др. Все эти пропорции можно получить из исходной
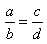
с помощью
этих правил.
1. В пропорции
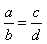
можно менять местами средние или крайние
члены или те и другие.
Получаем:
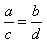 ;
;
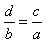 ;
;
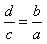 .
.
2. В пропорции можно менять местами предыдущие и последующие члены обоих ее отношений. Из
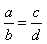
получается
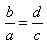
.
Эта пропорция
уже получена выше; (в виде
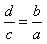
). Точно так же ничего нового
не получим, переставляя предыдущие и последующие члены в трех выше найденных пропорциях.
Производные пропорции. Если
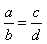
, то справедливы и
следующие пропорции (так называемые производные пропорции), получаемые из данной:
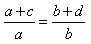 ;
;
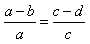 ;
;
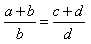 ;
;
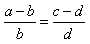 ;
;
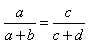 ;
;
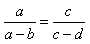 ;
;
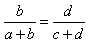 .
.
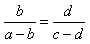 ;
;
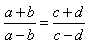 ;
;
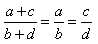 ;
;
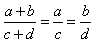 ;
;
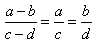 ;
;
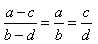 .
.
Эти и множество подобных им производных пропорций могут быть объединены в двух основных формах:
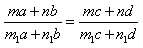 , (1)
, (1)
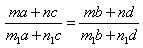 , (2)
, (2)
где m, n, m1, n1 – любые числа*.
Так полагая в формуле (1) m = n = m1 =1, n1=0, получим производную пропорцию
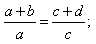
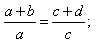
полагая в формуле (2) m = n = m1 =1, n1=0, имеем
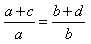
или, переставляя средние члены,
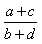
=
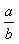
и т. д.
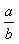 *Форма (2) может быть получена по тому же правилу, что и (1), если предварительно переставить средние члены в данной
пропорции.
*Форма (2) может быть получена по тому же правилу, что и (1), если предварительно переставить средние члены в данной
пропорции.
![]() вытекает ad=bc (произведение средних членов равно произведению
крайних); обратно, из ad=bc вытекают пропорции
вытекает ad=bc (произведение средних членов равно произведению
крайних); обратно, из ad=bc вытекают пропорции
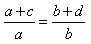 ;
;
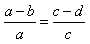 ;
;
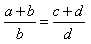 ;
;
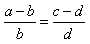 ;
;
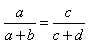 ;
;
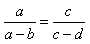 ;
;
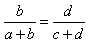 .
.
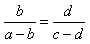 ;
;
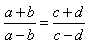 ;
;
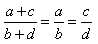 ;
;
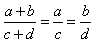 ;
;
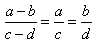 ;
;
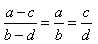 .
.
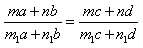 , (1)
, (1)
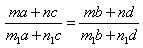 , (2)
, (2)
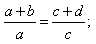
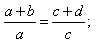 полагая в формуле (2) m = n = m1 =1, n1=0, имеем
полагая в формуле (2) m = n = m1 =1, n1=0, имеем 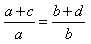 или, переставляя средние члены,
или, переставляя средние члены, 